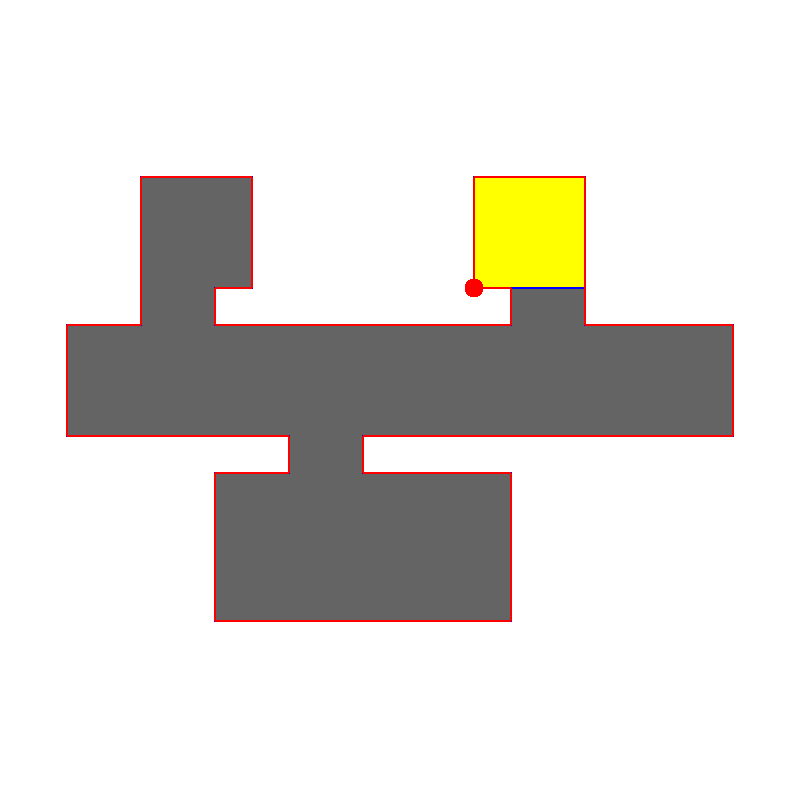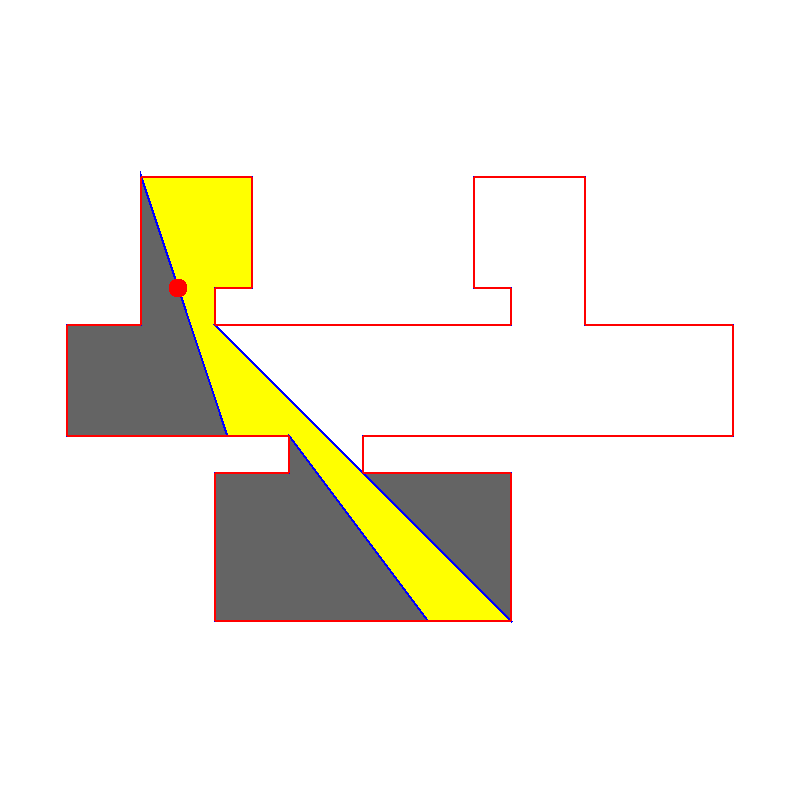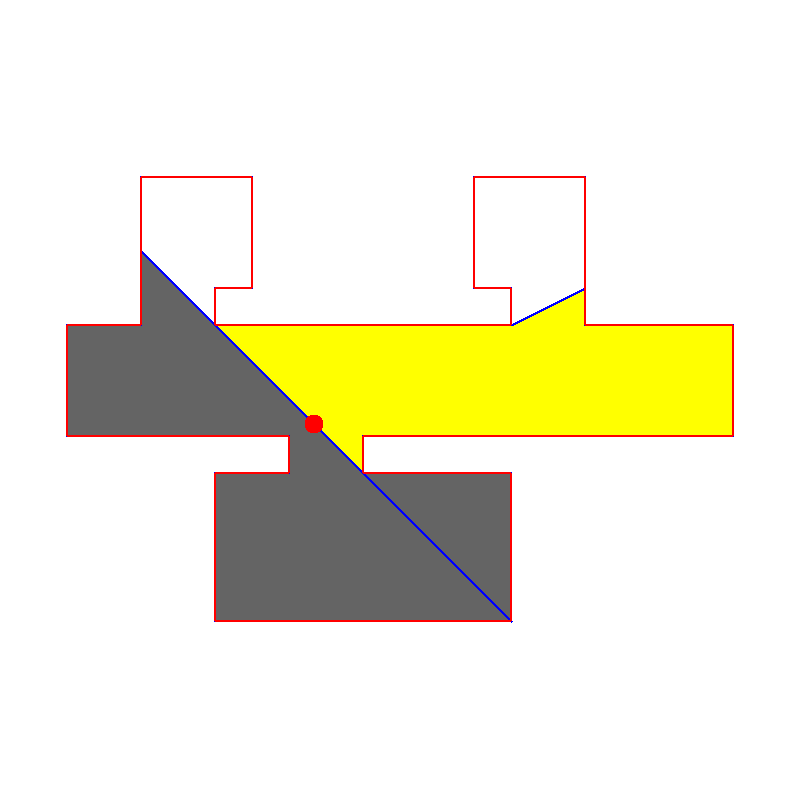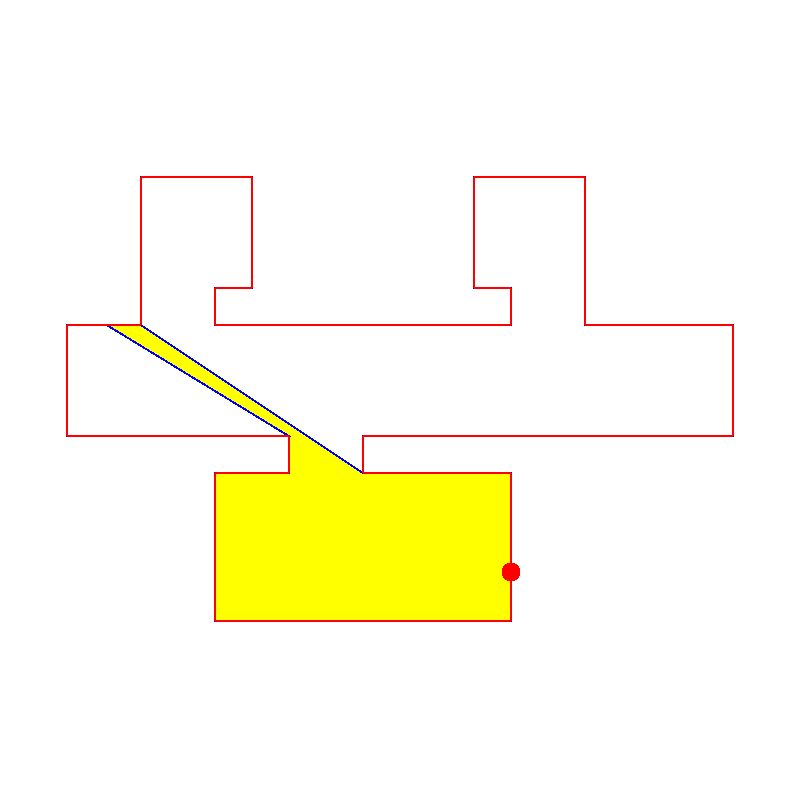Ian Edgerton mente Charlie kunne hjælpe ham, og det kunne han minsandten.
Matematikken var Pursuit-Evasion, som vi har haft tidligere på bloggen, der var spilteori, Charlie nævnte syntetisk differentialgeometri som en analogi til noget svært, tror jeg nok, der var “Longitudinal socialization process” og en del om mønstre og netværk.
Pursuit Evasion
Det kan dække over flere ting. Jeg har skrevet om det i afsnittene To døtre, Spree og Mørkt Stof
En version af Pursuit Evasion drejer sig om en forfølger og et bytte. Forfølgeren kan se byttet, og løber hele tiden hen mod byttet. Hvordan det ender, omme an på, hovr hurtigt, de begge løber, og hvilken kurve, byttet løber på.
Hvis byttet løber på en linje, er forfølgerens kurve en tractrice, eller hundekurve:
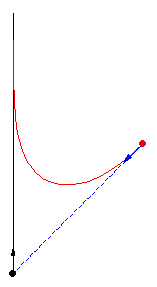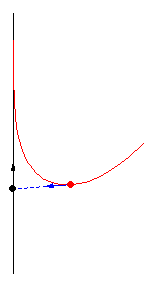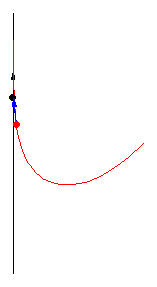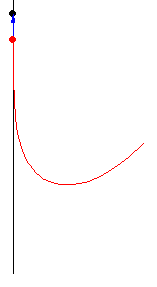
Her er forskellige eksempler, hvor byttet løber på en cirkel med konstant fart:
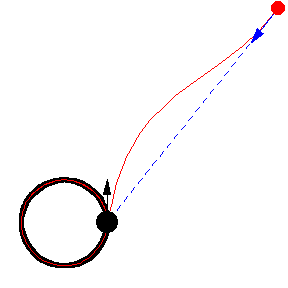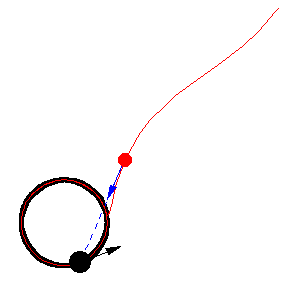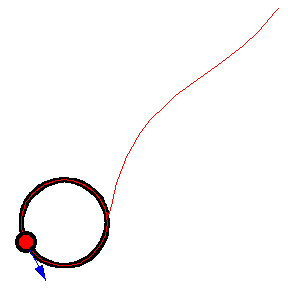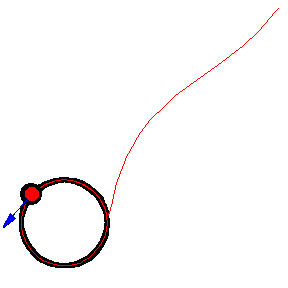
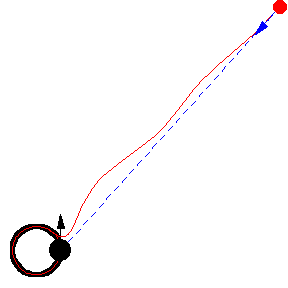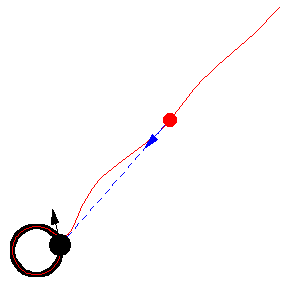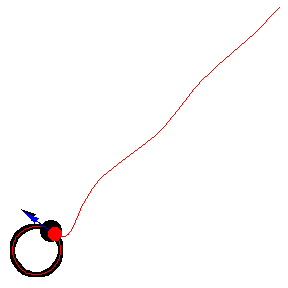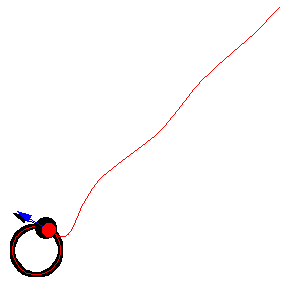
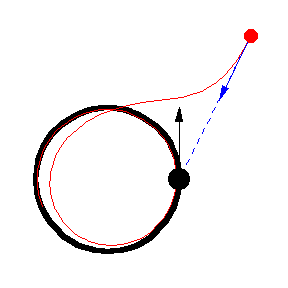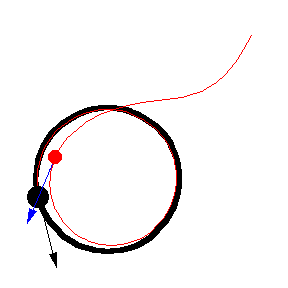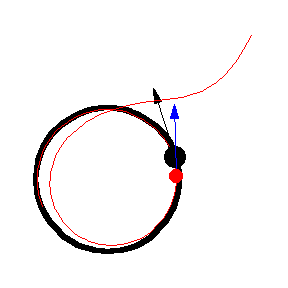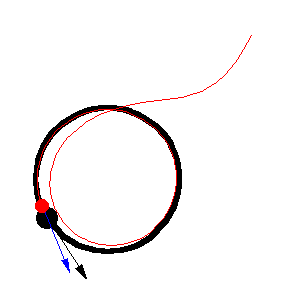
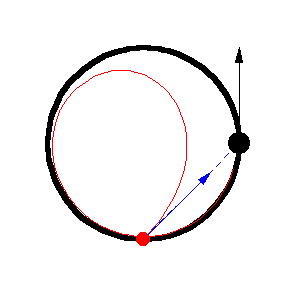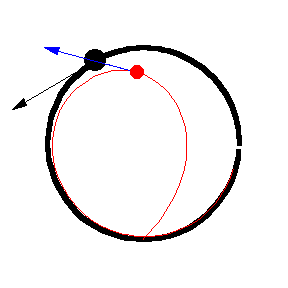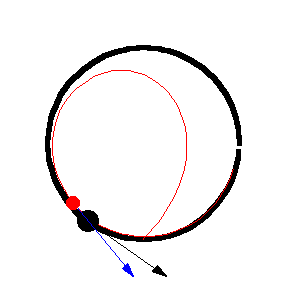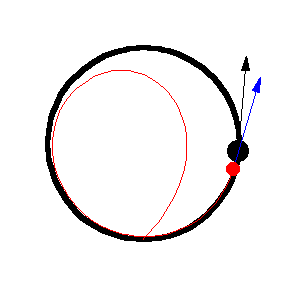
Illustrationerne er fra Mathworld. I kan læse om ligningerne bag – differentialligninger – på “Spree” linket, men jeg kopierer det ind her som en service 🙂
Vi beskriver en kurve i planen ved en parameterfremstilling: (x(t),y(t)), hvor t er tiden. Man kan altså løbe på en linie ved f.eks.
x(t)=t
y(t)=2t+3
Så er man i punktet (2,7) til tiden t=2, og man er i (0,3) når t=0, og man løber med konstant fart. Man kan løbe på den samme linie med f.eks.
x(t)=t^3
y(t)=2t^3+3
hvor t^3 betyder t i tredie.
Her er man stadig i (0,3) når t=0, men man er i (8,19), når t=2. Man løber ikke med konstant fart.
Kald nu forfølgerens kurve
F(t)=( f1(t), f2(t))
og undvigerens
U(t)=(u1(t),u2(t))
Betingelsen om “ren” forfølgelse – pure pursut – siger, at vektoren
U(t)-F(t)=(u1(t)-f1(t),u2(t)-f2(t))
er parallel med forfølgerens hastighedsvektor – forfølgeren løber direkte mod byttet.
F’(t)=(f1′(t),f2′(t))
og man får således en differentialligning, som beskriver forfølgerens hastighedsvektor udfra forfølgerens position og undvigerens position. Hvis forfølgeren løber med konstant fart k, bliver ligningen
F’(t)=k(U(t)-F(t))/|U(t)-F(t)|
eller rettere
f1′(t)=k(u1(t)-f1(t))/|U(t)-F(t)|
f2′(t)=k(u2(t)-f2(t))/|U(t)-F(t)|
hvor |U(t)-F(t)| er længden af vektoren. Hvis vi nu kender U(t) – altså forfølgerens kurve – kan vi opstille ligningen. Vi har også resultater, der siger, at den slags ligninger har løsninger (under passende forudsætninger om U(t)), men generelt kan vi ikke skrive en løsning op med pæne formler.
Til gengæld kan vi få en computer til at regne en løsning ud stepvis: Man lader forfølgeren gå et lille stykke langs linien, der peger mod undvigeren. I mellemtiden har undvigeren flyttet sig, så man får en ny linie, man løber et lillebitte stykke ad. Og så fremdeles. Man laver altså en kurve af små bitte stykke linie. Det kan gøres lidt mere intelligent, end beskrevet her, og man kan få en løsningskurve, der er så tæt på den rigtige, som man vil have det.
En anden version af pursuit evasion bruges, når man vil have robotter til at afsøge et terræn. Robotterne har et vist synsfelt, de skal holde øje med et område, og ingen må undslippe. At beregne, hvor mange robotter, der minimum skal bruges til et givet område, er NP-hårdt. Det kan man læse mere om her på Stanford. Her er deres algoritme i brug på et ganske indviklet område. Der er en robot. Det gule er det, den kan se. Det hvide er sikkert, og det går kan stadig gemme “fjender