Jeg er lidt handicappet i denne uge: Vi er gået igang med sæson 4 og jeg har ikke fået DVD’erne, men de skulle være sendt, så i næste uge kan jeg igen se på Numb3rs i forvejen. Dette er skrevet, inden jeg har set afsnittet – så jeg ved ikke, om det er det væsentligste matematik i udsendelsen, men pyt.
Trust Metric
Titlen på afsnittet refererer til måling og udregning af tillid. Mere præcist drejer det sig om at automatisere effekten af, at man stoler mere på en person, som en ven siger god for, end på en tilfældig person. Man har brug for at automatisere den slags “videreførelse af tillid”, når man f.eks. skal vurdere udbydere på ebay eller websider. Google tildeler alle websider et tal, som er udregnet ved den berømte PageRank algoritme. PageRank af en webside afhænger af, hvor mange andre sider, der linker til siden og af, hvor mange, der linker til dem etc. Det vil jeg ikke beskrive nærmere her. Der er en beskrivelse på dansk her. Når man søger i Google er den side, der kommer først i resultatet, den, der indeholder søgeordet og har højst Pagerank. Man kender ikke helt algoritmen bag Page Rank – den er patenteret og delvis hemmelig, så man ikke kan snyde den, eller det i hvert fald er svært at få sin www side op øverst ufortjent.
Illuminations problemet
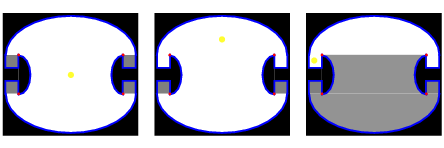
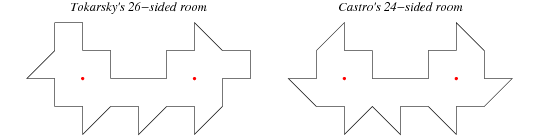
Man forestiller sig et rum, hvis vægge er lavet af spejle, som reflekterer lyset. Kan man så altid finde et punkt, hvor man kan placere en lyskilde, så lyset når ud til alle andre punkter. Kan man måske nå ud til alle punkter ligegyldigt, hvor man placerer lyskilden?
Svaret afhænger selvfølgelig af rummets facon. I 1958 konstruerede Roger Penrose et eksempel på et rum, der altid ville have mørke områder, lige gyldigt hvor, man placerede en lyskilde.